轻松一刻😉

概述

# 算法复杂度

算法复杂度是在计算在输入量为 N 的情况下，算法的[空间使用]和[时间使用]情况。体现算法运行使用的时间与空间随[数据大小 N]而增大的速度。

算法复杂度主要从时间和空间两个角度评价：

时间：假设各操作的运行时间为固定常数，统计算法运行的「计算操作的数量」，以代表算法运行所需时间；
空间：统计在最差情况下，算法运行所需使用的「最大空间」；

「输入数据大小 N 」指算法处理的输入数据量；根据不同算法，具有不同定义，例如：

排序算法： N 代表需要排序的元素数量；搜索算法： N 代表搜索范围的元素总数，例如数组大小、矩阵大小、二叉树节点数、图节点和边数等；

# 时间复杂度

根据定义，时间复杂度指输入数据大小为 N 时，算法运行所需花费的时间，需要注意：

统计的是算法的[计算操作数量]，而不是[运行的绝对时间]。计算操作数量与运行绝对时间呈正相关关系，并不相等。算法运行时间受到「编程语言、计算机处理器速度、运行环境」等多种因素影响。
体现的是计算操作随数据大小 N 变化时的变化情况。根据定义，时间复杂度指输入数据大小为 N 时，算法运行所需花费的时间。需要注意：

# 符号表示

根据输入数据的特点，时间复杂度具有「最差」、「平均」、「最佳」三种情况，分别使用 O , Θ , Ω 三种符号表示。

# 常见种类

根据从小到大排列，常见的算法时间复杂度主要有：

O(1)<O(logN)<O(N)<O(NlogN)<O(N^2)<O(2^N)<O(N!)

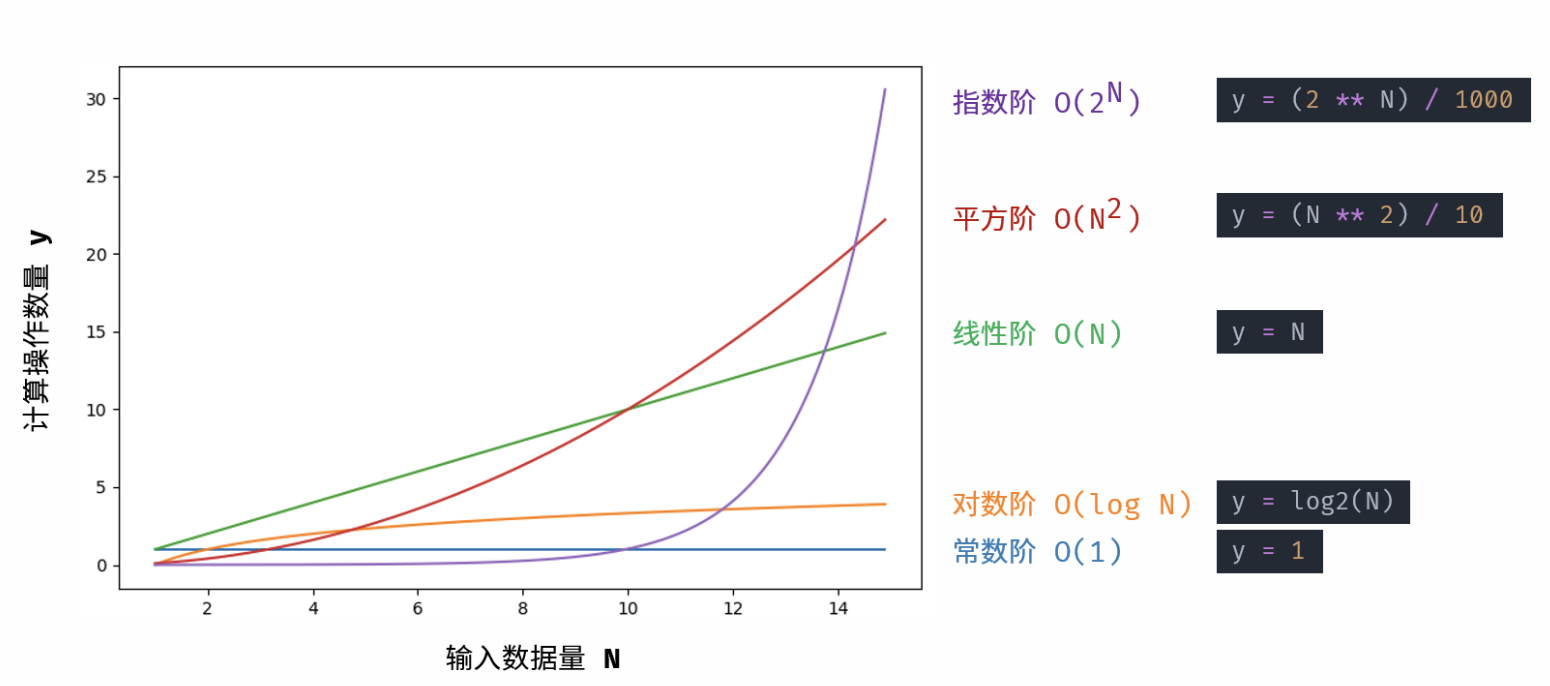
常数 O(1) ：运行次数与 N 大小呈常数关系，即不随输入数据大小 N 的变化而变化。(计算操作数量:1)
线性 O(N)：循环运行次数与 N 大小呈线性关系，时间复杂度为 O(N) 。比如 for 循环一次(计算操作数量:N)
平方 O(N^2) ：两层循环相互独立，都与 N 呈线性关系，因此总体与 N 呈平方关系，时间复杂度为 O(N^2) 比如冒泡排序：
指数 O(2^N)：细胞分裂。指数阶常出现于递归

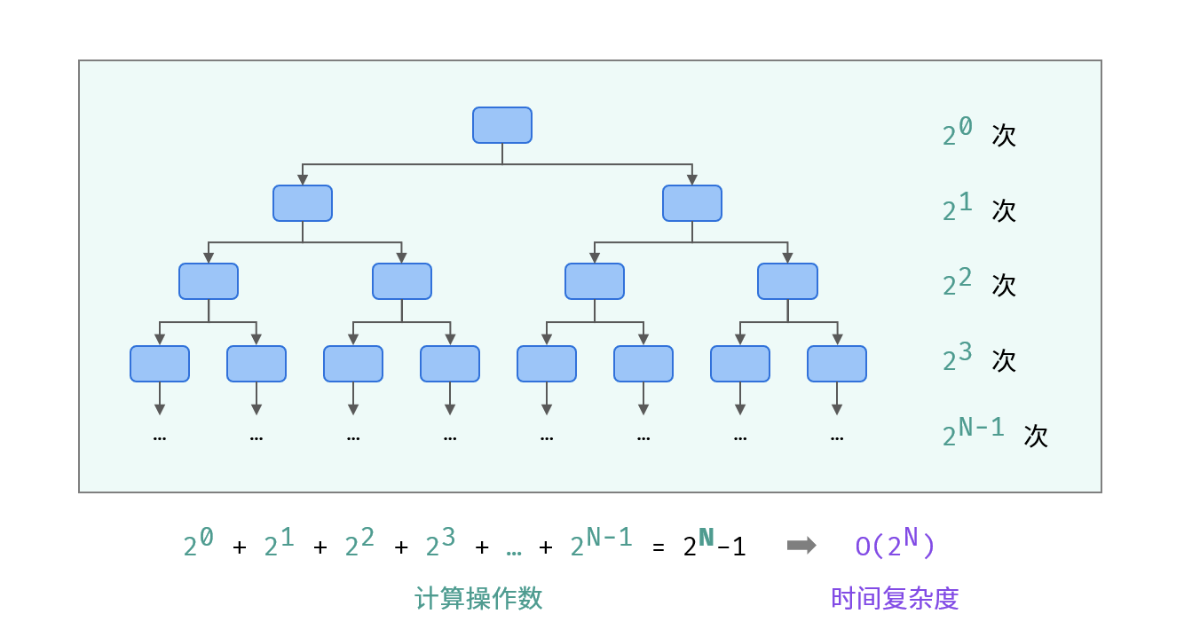
阶乘 O(N!)：阶乘阶对应数学上常见的 “全排列” 。即给定 N 个互不重复的元素，求其所有可能的排列方案。

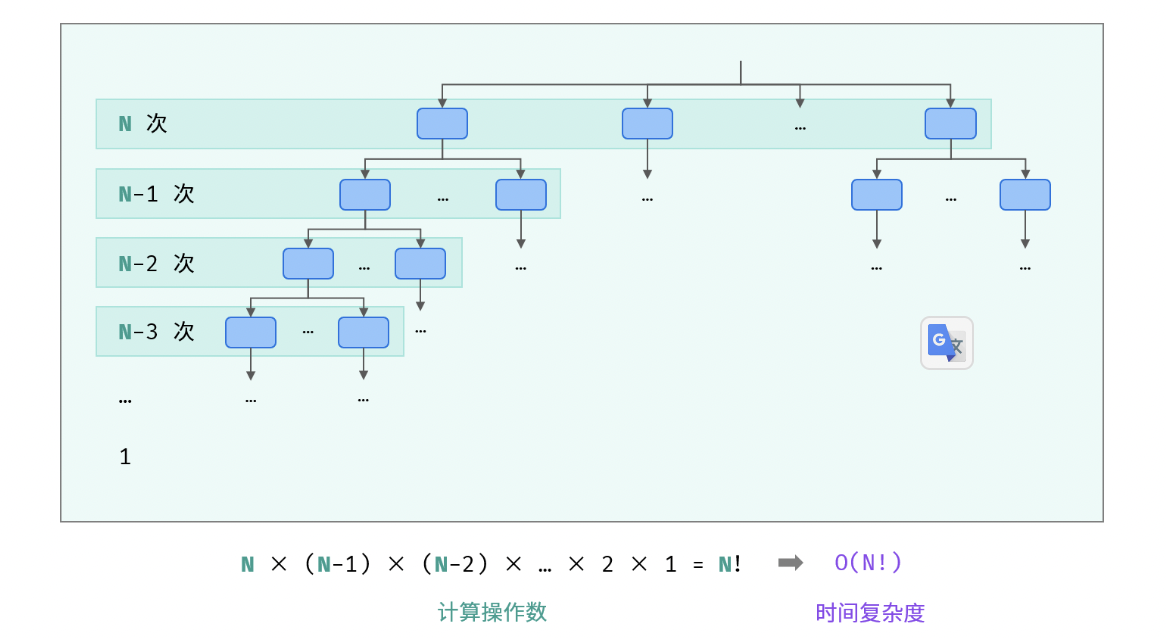
对数 O(log N) ：对数阶常出现于「二分法」、「分治」等算法中，体现着 “一分为二” 或 “一分为多” 的算法思想。

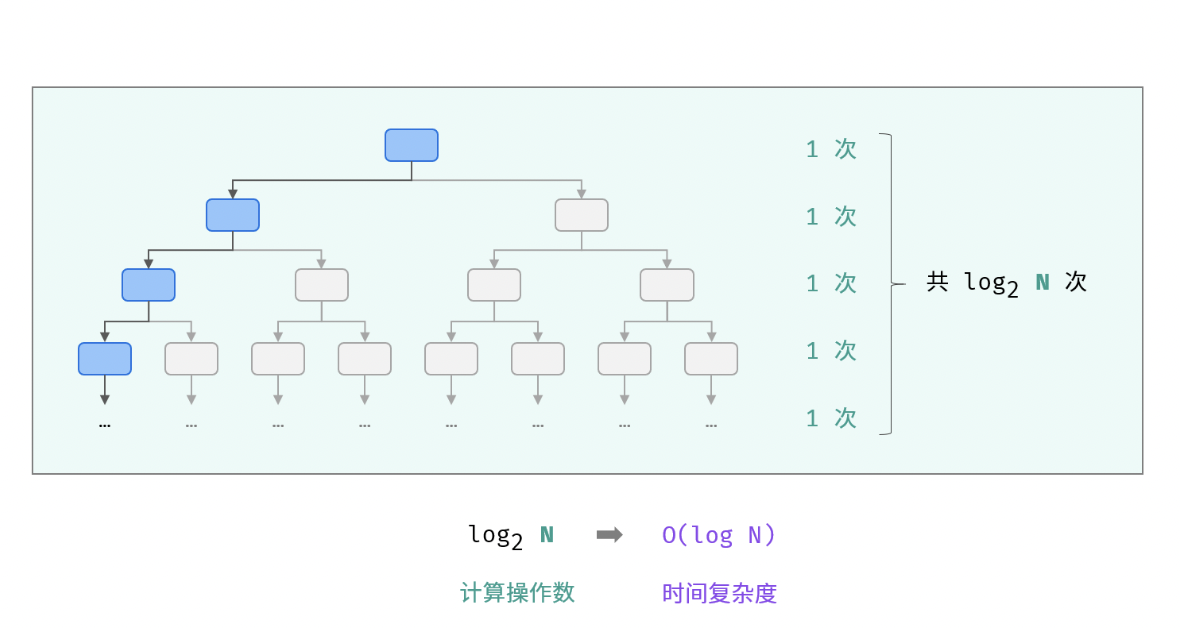
function algorithm(N):
    var count = 0,i = N,a = 3
    while (i > 1) {
      i = i / a
      count += 1
    }
    return count

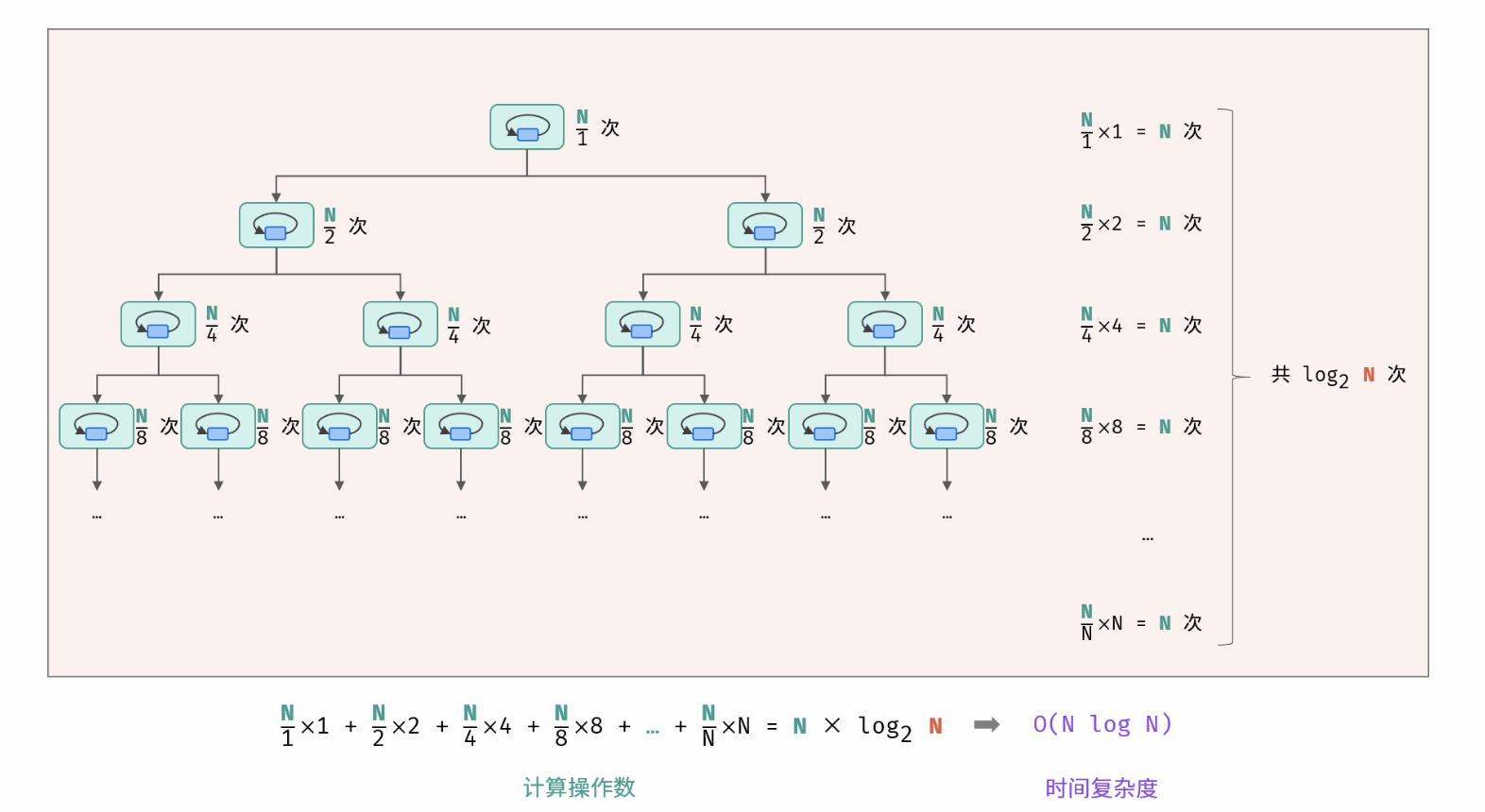
线性对数 O(Nlog N): 两层循环相互独立，第一层和第二层时间复杂度分别为 O(logN) 和 O(N)，则总体时间复杂度为 O(Nlog N)；

function algorithm(N) {
  var count = 0;
  i = N;
  while (i > 1) {
    i = i / 2;
    for (j in range(N)) {
      count += 1;
    }
  }
  return count;
}

线性对数阶常出现于排序算法，例如「快速排序」、「归并排序」、「堆排序」等.

# 空间复杂度

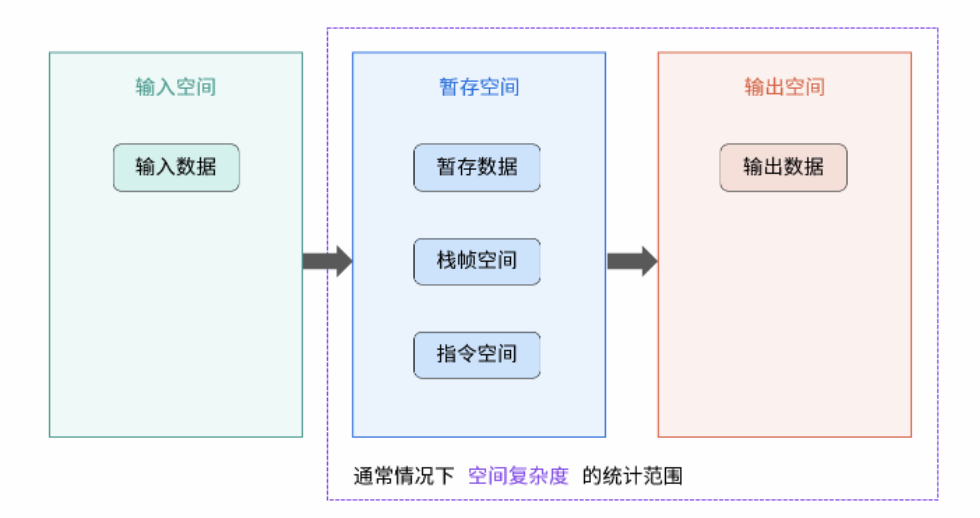
空间复杂度涉及的空间类型有：

输入空间：存储输入数据所需的空间大小；
暂存空间：算法运行过程中，存储所有中间变量和对象等数据所需的空间大小；
输出空间：算法运行返回时，存储输出数据所需的空间大小；

通常情况下，空间复杂度指在输入数据大小为 N 时，算法运行所使用的「暂存空间」+「输出空间」的总体大小。

指令空间：

编译后，程序指令所使用的内存空间。

数据空间：算法中的各项变量使用的空间，包括：声明的常量、变量、动态数组、动态对象等使用的内存空间。
栈帧空间：

程序调用函数是基于栈实现的，函数在调用期间，占用常量大小的栈帧空间，直至返回后释放。如以下代码所示，在循环中调用函数，每轮调用 test() 返回后，栈帧空间已被释放，因此空间复杂度仍为 O(1) 。

function test() {
    return 0;
}

function algorithm(N) {
    for (var i = 0; i < N; i++) {
        test();
    }
}

算法中，栈帧空间的累计常出现于递归调用。如以下代码所示，通过递归调用，会同时存在 N 个未返回的函数 algorithm() ，此时累计使用 O(N) 大小的栈帧空间。

function algorithm(int N) {
    if (N <= 1) return 1;
    return algorithm(N - 1) + 1;
}

# 常见种类

根据从小到大排列，常见的算法空间复杂度有：

O(1)<O(logN)<O(N)<O(N^2)<O(2^N)

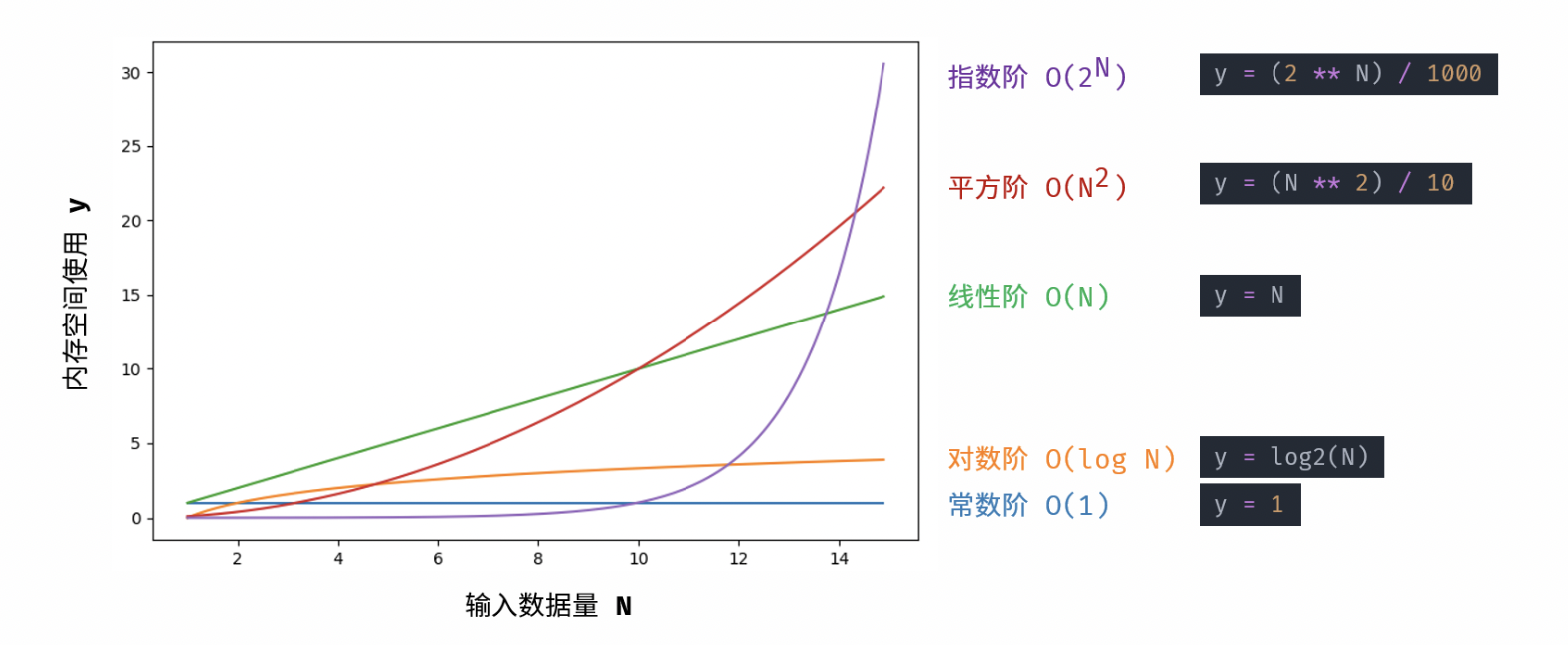
常数 O(1)：普通常量、变量、对象、元素数量与输入数据大小 N 无关的集合，皆使用常数大小的空间。
线性 O(N) ：元素数量与 N 呈线性关系的任意类型集合（常见于一维数组、链表、哈希表等），皆使用线性大小的空间
平方 O(N^2)：元素数量与 NN 呈平方关系的任意类型集合（常见于矩阵），皆使用平方大小的空间
指数 O(2^N)：指数阶常见于二叉树、多叉树
对数 O(logN)：对数阶常出现于分治算法的栈帧空间累计、数据类型转换等，例

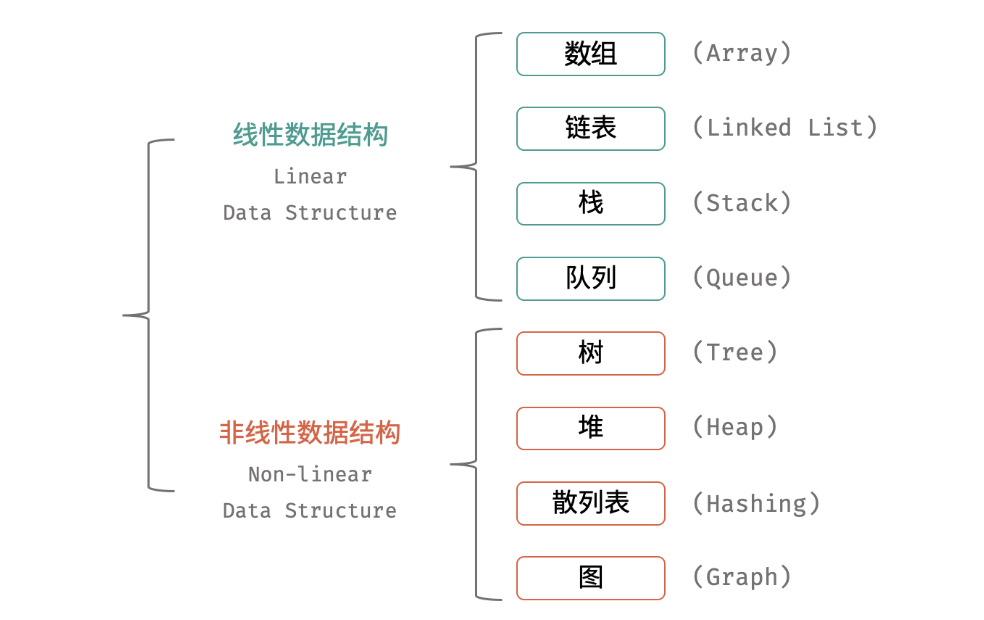
# 数据结构简介

常见的数据结构可分为[线性数据结构]与[非线性数据结构]，具体为：「数组」、「链表」、「栈」、「队列」、「树」、「图」、「散列表」、「堆」。

#基础

剑指offer→